
Finite Fields
- 04 Dec, 2024 |
- 02 Mins read
Finite fields is so interesting.
But first what is a field? You could look that up on Wikipedia, there is no value in this post explaining that.
Perhaps what is more valuable is the motivation behind a field!
A laymen’s attempt on motivation behind fields.
You just came back from Japan.
- Japan was clean
- Japan has great public transport
- Japan had great food
You liked it and would like something simillar for your next vacation.
I like countries that are
- clean
- has great public transport
- has great food
Likewise in mathematics, we have different “number systems” (comparable to countries). We would like to preserve some “rules” (comparable to qualities) that makes it nice to work with!
We like number systems that have
- addition and multiplication
- identities and inverses for addition and multiplication
- additive and multiplicative commutativity
- are self-contained
But why do you like these in particular?
Well, maybe it will become apparent during the worked examples.
Example of fields?
Real numbers
-
we can add and multiply them
-
additive and multiplicative inverses exist!
the additive inverse is simply the negative version of numbers
the multiplicative inverse is simply the reciprocal of the number
-
reals are self contained (examples for non-fields will shine more light on this)
Example of Non-fields?
Integers
- we can add and multiply them
- additive inverse exist!
the additive inverse is simply the negative version of number
- multiplicative inverse does not exist
the multiplicative inverse is the reciprocal of the number, however the reciprocal is ==NOT AN INTEGER!==
- Integers are not self contained
If we were to divide an integer with another integer , we might require another class of numbers (namely rationals), to describe the answer
Enter Hero (Stage Left) i.e. Finite Fields
Integers can be finite fields.. just use modular arithmetic!
The catch is we have to use prime/powers of prime as modulus numbers!
let’s consider modulus 5
the additive inverse of 3 is 3.. because
the multiplicative inverse of 3 is 2.. because
here’s the multiplication table for modulo 5
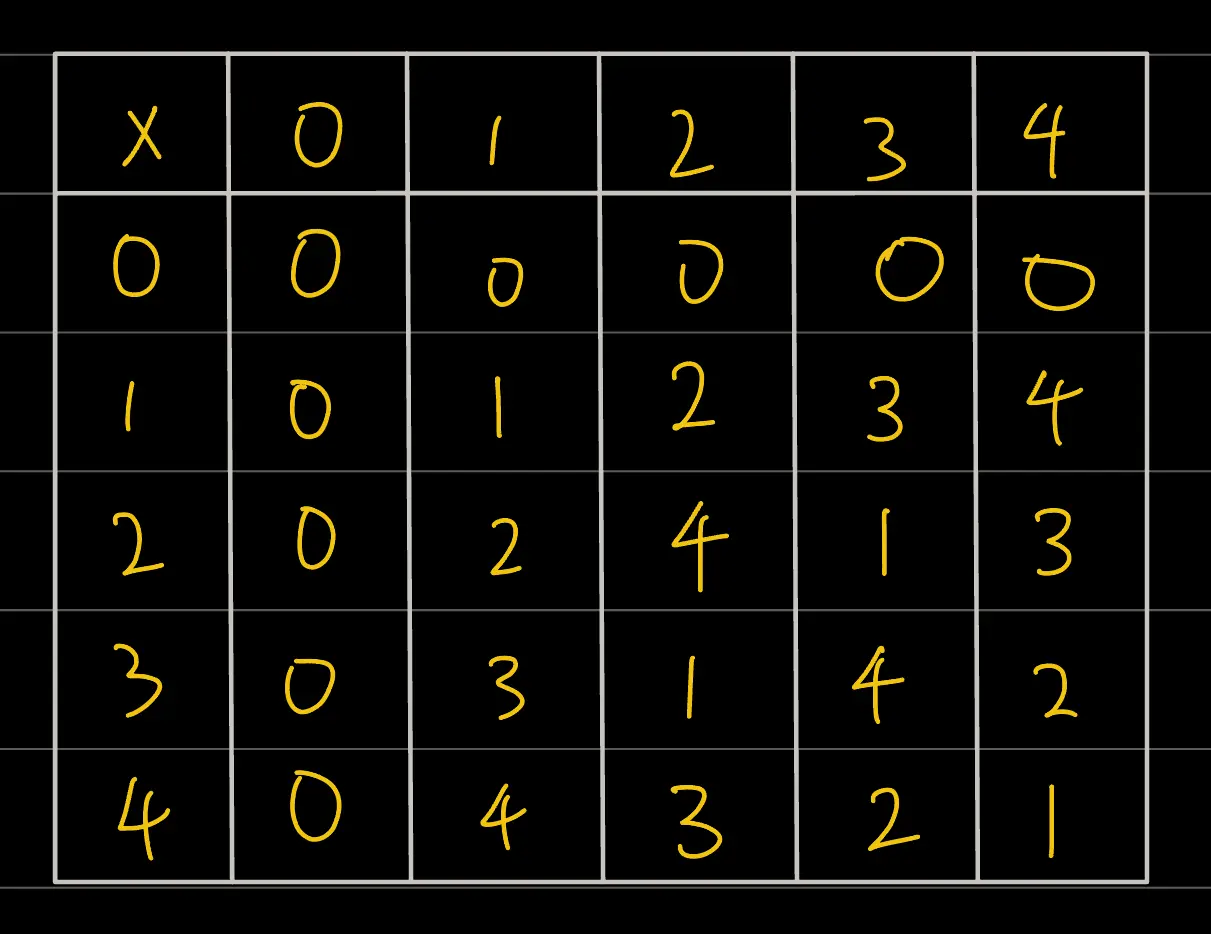
here’s an interesting observation: except the rows and columns with zeroes, all the rest have all the numbers 01234 appearing exactly once
kinda like sudoku!
what if we tried doing this with modulo 6 (which is not a prime and not a power of a prime)?
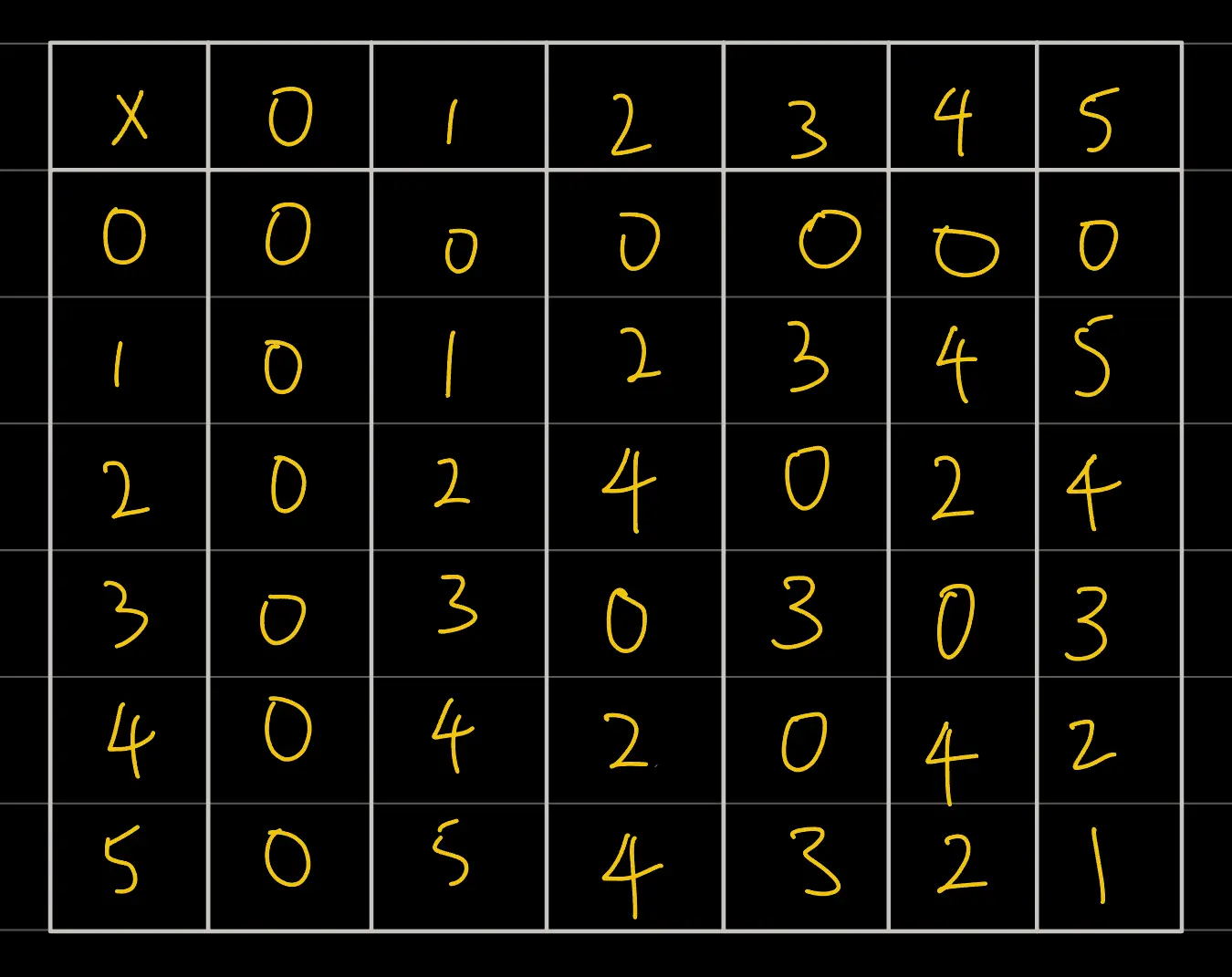 it no longer has that sudoku qualities
it no longer has that sudoku qualities
which means multiplicative inverses may not exists for all numbers!
for example 2 has no multiplicative inverse.. because
let
caption: if we put into a box, the values of x that satisfy 2x = 1(modulo 6), we would get an empty box